How to Interpret Water Borehole Pumping Test
There are several ways of analyzing pumping test data, (The table below show the commonly used methods for pumping-test data analysis).
| SN | Type of Aquifer | Type of Pumping test data | Names of methods |
|---|---|---|---|
| 1 | Confine Aquifer | I. Time Drawdown data II. Unsteady distance drawdown data III. Quasi-Steady/ Steady Distance drawdown data IV. Recovery Data: – Time Residual Drawdown data – Time Recovery Data | – Theis Type curve method – Cooper-Jacob Straight line method Cooper-Jacob Straight line method – Thiem method – Graphical method – Residual Drawdown-Time Ratio method – Cooper-Jacob Straight line method |
| 2 | Unconfined Aquifer without Delayed Yield | I. Time Drawdown data II. Unsteady distance drawdown data III. Quasi-Steady/ Steady Distance drawdown data IV. Recovery Data: – Time Residual Drawdown data – Time Recovery Data | – Theis Type curve method – Cooper-Jacob Straight line method Cooper-Jacob Straight line method – Thiem method – Graphical method – Residual Drawdown-Time Ratio method – Cooper-Jacob Straight line method |
| 3 | Unconfined Aquifer with Delayed Yield | I. Time Drawdown data II. Quasi-Steady/ Steady Distance drawdown data | – Type-Curve method – Newman Straight Line method – Thiem method – Graphical method |
| 4 | Leaky Confined Aquifer without Storage in Aquitards | I. Time Drawdown data II. Quasi-Steady/ Steady Distance drawdown data | – Walton Type curve method – Hantush Inflection Point method – Type-Curve method |
| 5 | Leaky Confined Aquifer with Storage in Aquitards | I. Time Drawdown data II. Quasi-Steady/ Steady Distance drawdown data | – Hantush Type Curve method – Type-Curve method |
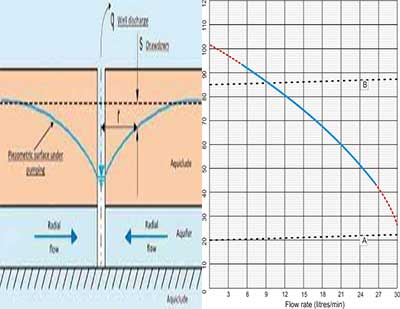
Some of these methods are quite sophisticated. However, for the purpose of this guidance note, what is important to the Supervisor is whether the borehole will deliver the required amount of water for the required pumping duration or not. The specific capacity of the borehole, which expresses the relationship between the yield and the drawdown, is the most important quantity of pumping test. (Step Test, Constant Rate Discharge Test and Recovery Test).
Specific Capacity=yield /drawdown (m3/hr. per meter drawdown)
By calculating the drawdown incurred by different pumping rates, and comparing that drawdown to the available vertical interval between the rest water level and the top of the well-screen (while allowing for likely seasonal water level variations, the effects of extended dry periods, and the interval occupied by the pump itself) it is relatively easy to determine a viable discharge for the well and whether the borehole can deliver sufficient water.
Calculation of Water Borehole Specific Capacity
| A pumping test was run for 24hours with a yield of (2,500 m3/hr.) and the drawdown (21 meter) were measured. The Specific Capacity is calculated as 2,500 m3/hr. divided by 21 meter, or 119 m3/hr. per meter |
The Specific Capacity obtained just after a well is drilled and properly developed is typically the highest value that will be produced and is the benchmark with which to compare all future values. As time goes by, the Specific Capacity will decline as plugging of the well’s perforations or filter pack occurs, as the pump starts to fail, or as static water levels change.
Specific Capacity tests should be performed at least semi-annually and water levels (static and pumping) should be collected monthly to provide early detection of potential well problems. Rehabilitation work should be initiated when a well’s Specific Capacity drops by 25% (Driscoll, 1986).
Specific capacity can also be used to provide the design pumping rate or maximum yield for the well as follows:
Calculation of Water Borehole Maximum Yield
| For example, the specific capacity of a borehole is 27 m3/hr. Assuming that only 15 m of drawdown is available in the well, the maximum yield is calculated as the Specific Capacity times the maximum drawdown, or 27 m3/hr * 15 m, = 405 m3/hr. This should be verified with other pumping test method. |
Calculation to determine if the borehole maximum specific capacity is enough to meet the need of the population end user.
As previously mentioned, the most important result of pumping test is to determine that the borehole flow for the required pumping duration is sufficient to meet the daily need of the population (maximum exploitable flow):
- Less than 14 hours in operation, the borehole is sufficient to meet the need of the population.
- Between 14 hours and 18 hours operation, bear in mind that the borehole may become too small in the near future due to population growth or reduced water levels in the aquifer due to prolonged exploitation. Furthermore, using the borehole becomes more expensive.
- Over 18 hours operation. The borehole does not meet the needs of the population. Depending on the circumstances, you can decide whether or not to equip the bore or drill another borehole. (Arnalich-water and habitat 2011).
| Calculation example: A borehole has been drilled for semi-urban population of 8000 people. The pumping test reveals that the maximum capacity of the borehole is 11 l/s. Is this enough to meet the needs of the population assuming 100 liters per person per day? With a daily demand of 100 liters per person, the quantity of water consumed is: 8,000 people * 100 l/person* day = 800,000 liters daily demand. The hourly production is: 11 l/s * 3600 s/hour = 39,600 l/hr The required number of operating hours is 800,000 l / 39,600 l/hr = 20.2 hours. The borehole is too small to meet the needs of the population. |
Approximate Calculation of Operating cost
Given a certain maximum capacity of the borehole, you can calculate operating cost.
The main expense is derived from energy consumption. To determine whether the population is able to pay for the operating cost of the borehole, calculating the energy consumption cost is usually sufficient.
e = mgh/3.6 ∗ 10⁶ η ∗ cost rate per kWh for local electricity tariff
Where:
m = mass of water per day in kg (1 liter of water weighs 1kg)
h = the pumping height taken from the lowest drawdown point to the water surface at the point of delivery.
g = gravity of acceleration on the surface of the earth at sea level is 9.8 m/s2
η = total efficiency for the pump, around 60% (for frictional losses use value of 0.5 (50%).
As generator are frequently required, you need to know the unit fuel cost of the diesel. The average fuel consumption of a generator is 0.3 liters of diesel per kwh produced.
| Calculation example: A borehole powered by a generator pumps 60,000 liters per day to a tank with a tank stand situated at elevation of 35m. The dynamic height of the borehole is 44m and the cost of diesel is #250 per liter. How much will it cost to pump a day? The pumping height is 35m + 44m = 79m. The energy consumed is: e = mgh/3.6 ∗ 10⁶ η = 60000 ∗ 79m ∗ 9.8m/ s² / 3.6 ∗ 10⁶ ∗ 0.5 = 25.8 kwh The number of liters of diesel required is: 25.8 kwh * 0.3 liters diesel / kwh = 7.74 liters The daily cost for the local population is: 7.74 liters * #250 /liter = #1,935 |
Water Borehole Transmissivity and Storage Coefficient
Data from constant-rate tests can be analyzed to derive the transmissivity of the aquifer. The storage coefficient of the aquifer can be calculated only if data from observation boreholes are available.
The goal of a recovery test, as in any aquifer test, is to estimate hydraulic properties of an aquifer system such as transmissivity, hydraulic conductivity and storativity (storage coefficient). One typically measures recovery after the termination of a constant-rate or step-drawdown pumping test to provide additional data for estimating aquifer properties.
| If transmissivity value of 10 m2/day is calculated from pumping test analysis, the question is, what does that value mean? Is a value of 10 m2/day good or bad? |
The answer mainly depends on what the intended yield of the borehole is. MacDonald et al (2005) carried out modelling using typical assumptions and parameters applicable to emerging countries, and came to the conclusion that for a borehole supplying 5,000 litres per day (20 litres per person for 250 people), the transmissivity value of the aquifer should be at least 1 m2/day.
An aquifer with a transmissivity value of 10 m2/day would be capable of yielding around 40,000 litres per day. By comparison, a public water-supply borehole in a typical sandstone aquifer capable of yielding about two million litres per day would have a transmissivity value of 300 to 400 m2/day when tested. Highly productive aquifers, capable of supporting major abstractions, can have transmissivity values of 1,000 to 2,000 m2/day.
Talk to us for your upcoming Water Borehole Pumping Test Project
Geodata Evaluation & Drilling LTD. offers water borehole pumping test services. Let us handle the project for you. contact us at www.geodatadrilling.com Phone: +234 8037055441